本帖最后由 free 于 2022-2-18 10:41 编辑
二维旋转推导假如有一个矢量(ρ,θ),那么在二维直角坐标系中可以得到x=ρ*cosθ y= ρ*sinθ;现在把这个矢量旋转β度,直角坐标系下变换后的矢量为(ρ,θ+β)其坐标值为x'= ρ*cos(θ+β) y'= ρ*sin(θ+β),得到x'= ρ*(cosθcosβ - cosθsinβ),y'= ρ*(sinθsinβ+sinθcosβ),由此得到x'= x*(cosβ - sinβ),y'= x*(sinβ+cosβ)
有了二维推导,我们可以得出三维变换 三维变换原理由用于齐次坐标表示,三维几何变换的矩阵是一个4阶方阵,其形式如下:

其中,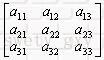   产生按轴缩放、旋转、错切等变换。 产生按轴缩放、旋转、错切等变换。 产生平移变换, 产生平移变换,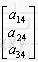     产生投影变换, 产生投影变换,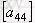   产生整体的缩放变换。 产生整体的缩放变换。
绕Z轴旋转φ得到举证表达式:
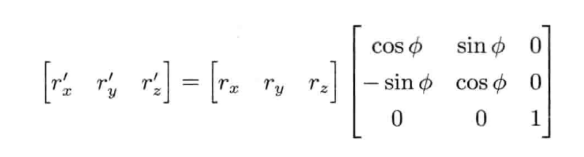
绕X轴旋转
绕Y轴旋转

平移  假设x轴的平移为tx, y轴的平移为ty,z轴的平移为tz,那么表示为:
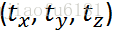  单轴缩放  假设x轴的缩放因子为sx, y轴的缩放因子为sy,z轴的缩放因子为sz,那么表示为: 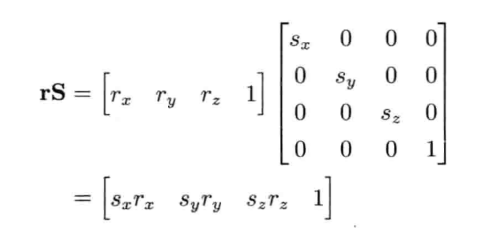 
|